ちょっとホモグラフィ変換について調べたので,そのまとめ(という名のいろんなページの情報集約)
ホモグラフィ変換とは
平面から平面へ写像する変換,ぐらいの理解.直感的には以下のサイトの下の方のデモアプリがわかりやすい.
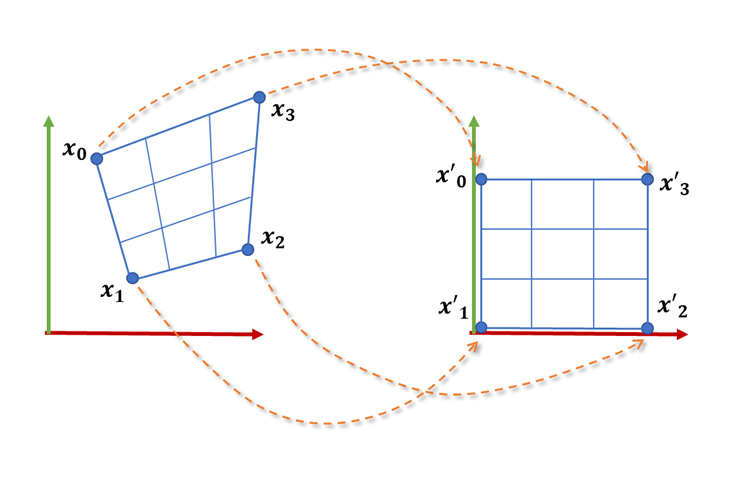
アフィン変換は,平行移動と回転・拡縮(スケール)・せん断(スキュー)の組み合わせまで.ホモグラフィ変換はそれを拡張し,台形のような変換まで可能.
結局は写像なので,以下のような同次変換で表すことができる.
ただし, は変換後の点,
は変換前の点とする.
ホモグラフィ変換行列  の導出
の導出
方針
ホモグラフィ変換行列を一般的に考えると,点の変換(
)は以下のように表せる.
ここで,を定数倍した,
(
は定数)での変換を考えると,結局
,
,
が
倍されるだけになる.
なので,この一般的なホモグラフィ変換行列はスケールに不定なので,これから考えるホモグラフィ変換行列は
を1として考える.つまり,
ここで求めるべき値はの8つの要素となる.1点の変換につき,
,
の2式が立てられるので,4点の変換がわかればホモグラフィ変換行列は求めることができるはず.
その4点を,変換前と変換後それぞれ (ただし,
])とし,それらは既知として,以下のような式を導出することで,
を求める.
式の展開
あらためて,元のこの式を から
への返還として展開すると,
とできる.よって,
第3式は両辺が同じ値になるので,第1, 2式を整理すると,
これを整理すると以下のようにでき,欲しい式のカタチになってきた!
残りの3点の変換も同様に考えると(というかコピペして並べると)以下の式になる.
ここまできたらあとは右辺行列の逆行列を求めて連立方程式を解けば,ホモグラフィ変換行列が求まる.
解き方としては,数学として解析的に解くか,実際にホモグラフィ変換を行うとき(= が既知のとき)に数値計算で解く,の2パターンがあると思う.
(なんか頑張れば解析的に逆行列求まらないかなぁと思いつつ,sympyでシンボリック計算をしてみたが終わらない...)
以下の実装例では,数値計算で解くパターン(OpenCV)と,特定の条件に絞って解析的に解くパターン(Unity)の2種類を示す.
実装例
OpenCV
この計算をそのままやってるのがOpenCVのgetPerspectiveTransform関数で,実際のソースは以下のようになっている.
srcに変換前の4点,dstに変換後の4点を入れると,ホモグラフィ変換行列を計算して返してくれる.
cv::Mat cv::getPerspectiveTransform(const Point2f src[], const Point2f dst[], int solveMethod) { CV_INSTRUMENT_REGION(); Mat M(3, 3, CV_64F), X(8, 1, CV_64F, M.ptr()); double a[8][8], b[8]; Mat A(8, 8, CV_64F, a), B(8, 1, CV_64F, b); for( int i = 0; i < 4; ++i ) { a[i][0] = a[i+4][3] = src[i].x; a[i][1] = a[i+4][4] = src[i].y; a[i][2] = a[i+4][5] = 1; a[i][3] = a[i][4] = a[i][5] = a[i+4][0] = a[i+4][1] = a[i+4][2] = 0; a[i][6] = -src[i].x*dst[i].x; a[i][7] = -src[i].y*dst[i].x; a[i+4][6] = -src[i].x*dst[i].y; a[i+4][7] = -src[i].y*dst[i].y; b[i] = dst[i].x; b[i+4] = dst[i].y; } solve(A, B, X, solveMethod); M.ptr<double>()[8] = 1.; return M; }
連立方程式の行列を作って,solverで解いて,結果を返していることがわかる.
これを見てもやはり解析的に逆行列を出すことは難しいのかな...と思えてくる.
Unity
凹みさんが,Unityでのホモグラフィ変換を実装している
凹み先生によると,
入力座標が (0.0, 0.0)、(1.0, 0.0)、(1.0, 1.0)、(0.0, 1.0) と出来るため 8 次元連立一次方程式は割りと綺麗に解くことが出来ます
とのことで,実装は以下のような感じ.
float[] CalcHomographyMatrix()
{
var p00 = v00.viewPosition;
var p01 = v01.viewPosition;
var p10 = v10.viewPosition;
var p11 = v11.viewPosition;
var x00 = p00.x;
var y00 = p00.y;
var x01 = p01.x;
var y01 = p01.y;
var x10 = p10.x;
var y10 = p10.y;
var x11 = p11.x;
var y11 = p11.y;
var a = x10 - x11;
var b = x01 - x11;
var c = x00 - x01 - x10 + x11;
var d = y10 - y11;
var e = y01 - y11;
var f = y00 - y01 - y10 + y11;
var h13 = x00;
var h23 = y00;
var h32 = (c * d - a * f) / (b * d - a * e);
var h31 = (c * e - b * f) / (a * e - b * d);
var h11 = x10 - x00 + h31 * x10;
var h12 = x01 - x00 + h32 * x01;
var h21 = y10 - y00 + h31 * y10;
var h22 = y01 - y00 + h32 * y01;
return new float[] { h11, h12, h13, h21, h22, h23, h31, h32, 1f };
}
手計算したのだろうか...掃き出し法とかもう覚えとらんよ...
まぁ確かにホモグラフィ変換の用途として,プロジェクションに使う場合だと画像やレンダリング結果を歪ませるだけだし,画像中の歪んだものを補正する系だと射影先はスクリーン座標の端から端なので,射影元/射影先のどちらかはだいたいスクリーン座標系の(0, 0),(0, 1),(1, 0),(1, 1)なんだよなぁ.
一般的なホモグラフィ変換が使われるのは,カメラの内パラキャリブレーションとかSfMとか,結構マニアックなとこぐらいなのかな.