こちらの記事ではbool型変数によって,変数の編集可/不可・表示/非表示を制御していました
mu-777.hatenablog.com
が,本記事ではそれの拡張版で,int/enum,string,float型の変数によっても制御できるようにします.
(本記事だけで内容は完結してますので,前記事を事前に読む必要はありません)
つまり何ができるか,ということですが,
例えばこういう実装で
public class ConditionalDisableAttrTest : MonoBehaviour
{
public enum FlagEnum { A, B, C }
[Header("Enum control")]
public FlagEnum flagEnum = FlagEnum.A;
[ConditionalDisableInInspector("flagEnum", (int)FlagEnum.A)]
public string editableStrIfEnumA = "AAA";
[ConditionalDisableInInspector("flagEnum", (int)FlagEnum.B)]
public string editableStrIfEnumB = "BBB";
[ConditionalDisableInInspector("flagEnum", (int)FlagEnum.C)]
public string editableStrIfEnumC = "CCC";
}
こういう感じに編集可/不可を制御できたり,

FlagEnumの設定値によって,他の変数の編集可/不可を制御できる
こうすれば,
public class ConditionalDisableAttrTest : MonoBehaviour
{
[System.Serializable]
public struct TestStruct
{
public Vector3 p;
public Quaternion q;
}
[Header("String control")]
public string flagStr = "A";
[ConditionalDisableInInspector("flagStr", "A", conditionalInvisible: true)]
public TestStruct visibleStructIfA;
}
表示/非表示を制御できたりします.(自作クラス/構造体も可)

flagStrが”A”のときだけインスペクタに表示される
こういうことをしたくて「Unity インスペクタ 変数 動的」とかでググると,CustomEditorを使う方法が出てきます.
が,これだとCustomEditorで対応したクラスでしか使えない = 他のクラスの変数に使い回しができなくて,ちょろっと使いたいときに不便な感じです.
(プロダクトレベルとかで,しっかり作り込む場合はこちらの方がいいと思いますが)
ということで,今回はCustomEditorは使わずに,任意のクラスの変数に適用できるAttributeを使って実装しています.
正直Unityのエディタ拡張は全然詳しくないので,バグってたらすみません.
一通りの型で使えることは確認しましたが,漏れもあるだろうし,基本正常系しか確認できてません.他のAttributeとの組合せ時とかも未検証です(免責事項)
あまり複雑な実装はいらない,以下のようにシンプルにbool変数で制御するだけでよい,という方は,前記事をご覧ください
| 編集可/不可 |
表示/非表示 |
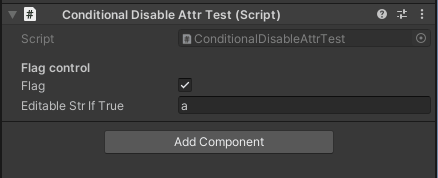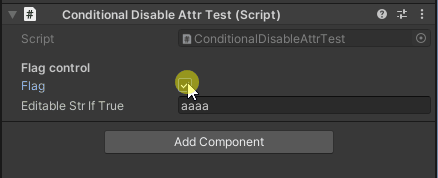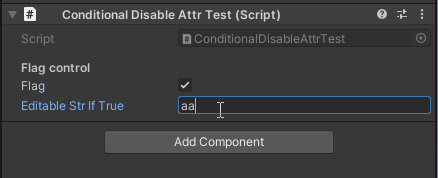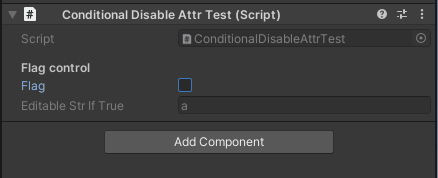 flagがfalseのときは編集不可になる flagがfalseのときは編集不可になる
|
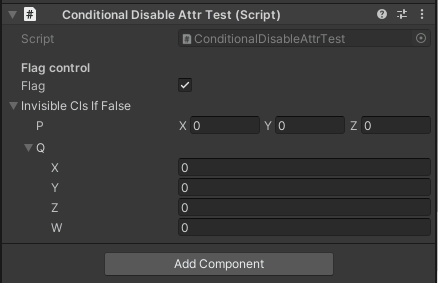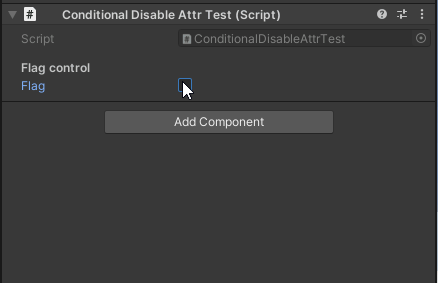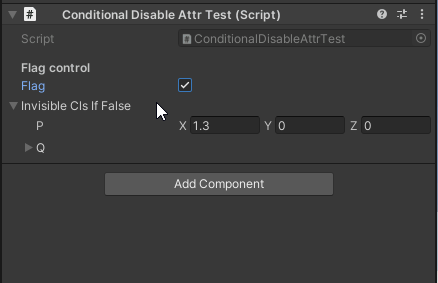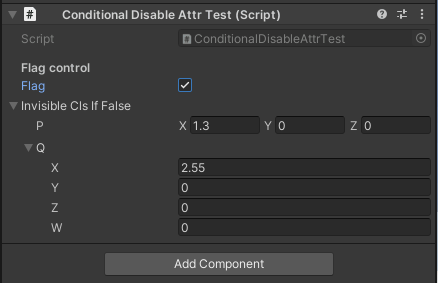 flagがfalseのときはインスペクタから見えなくなる flagがfalseのときはインスペクタから見えなくなる
|
続きを読む







